How do superconductors work
Superconductors, particularly high-temperature superconductors, hold a crucial role in the realm of superconducting wires, primarily owing to their critical current density and its sensitivity to magnetic fields. Despite their elevated critical temperatures, these high-temperature superconductors exhibit limitations in their critical current due to their intricate crystalline and microcrystalline structures, as well as the grain makeup of the material.
In essence, a high-temperature superconductor comprises a network of grains with commendable superconducting attributes, characterized by critical current densities approaching 106 A·cm–2 and impressive second critical fields of approximately 100 T. These grains are interconnected by interfaces displaying less favorable superconducting properties, where critical current densities fall within the range of 102 to 103 A·cm–2 and decrease even further when exposed to modest magnetic fields. It’s these interfaces that ultimately impose restrictions on the overall critical current values of the material.
Moreover, despite their ability to maintain high second critical fields, even at the temperatures achievable with liquid nitrogen, the practical utility of high-temperature superconductors is constrained by the presence of magnetization hysteresis concerning applied external magnetic fields. This hysteresis phenomenon is essential for enabling a given sample to conduct current without losses within a specific field and temperature range. Notably, a wider hysteresis corresponds to higher potential densities of superconducting current, capable of flowing without dissipation.
Interestingly, at elevated magnetic fields, the magnetization curve regains reversibility above a critical threshold known as the irreversibility field. Beyond this point, the sample can no longer conduct current without losses under these conditions. The temperature-dependent behavior of this irreversibility field forms what is known as the “irreversibility line” on the Hodwr(T) phase diagram, with the irreversibility fields generally being considerably smaller than the second critical field at a given temperature.
While bismuth superconductors are extensively used for crafting superconducting wires and tapes, they are limited to lower temperatures due to magnetic flux flow processes that result in losses when temperatures exceed those achievable with liquid nitrogen. The allure of thallium superconductors lies in their higher critical temperatures and significantly elevated irreversibility fields at liquid nitrogen temperatures when compared to bismuth superconductors.
Superconducting materials typically constitute only a fraction of a device’s volume and mass. Often, only the superconducting components are enclosed within a cryostat and cooled to cryogenic temperatures, while the remaining components of the device operate at ambient temperatures above 290 K. The distinctive attributes of superconductivity, including zero resistivity and perfect diamagnetism, are exhibited by certain metals and substances under specific conditions governed by temperature, magnetic field strength, and electric current.
These superconducting elements within devices can exist in a superconducting state either continuously, periodically, or sporadically. This state is achieved when the operating parameters, defined by temperature, current density, and magnetic field strength, fall below the material’s critical surface or critical characteristics. The critical surface, a function of temperature, current density, and polamagnetic intensity, plays a pivotal role in this context. Additionally, the critical characteristic of a superconductor relates to the dependency of critical magnetic field strength on current density (or vice versa) at a specific temperature.
Significantly, during the transition from the superconducting state to the resistive state, located above the critical surface or critical characteristics, superconducting materials undergo abrupt changes in their electrical and magnetic properties. This distinction has led to the classification of superconductors into two types, namely superconductors of the first and second type, based on their behavior in a magnetic field.
Application of high-temperature superconductors in current limiters
The emergence of high-temperature superconductors has ignited a surge of interest in their potential applications within the electric power industry, especially in the context of advancing power grids. A promising avenue for these ceramic high-temperature superconductors lies in their role as short-circuit current limiters, effectively safeguarding power grids from overloads and eliminating the need for costly equipment over-sizing. According to assessments conducted by the US Department of Energy (DOE), the US market alone anticipates a multi-billion-dollar potential for superconducting current limiters over the next fifteen years, with commercial utilization expected in the next three to five years.
These systems harness the unique attributes of superconductors, capitalizing on their rapid response to changes in magnetic induction and resistivity as the current surpasses a critical threshold. In essence, superconducting tapes can be regarded as “smart” materials due to their capacity to swiftly transmit current without losses under normal operating conditions while promptly identifying and reacting to excessive current pulses, a feat beyond the capabilities of conventional materials like copper wires.
One major advantage of employing superconductors in short-circuit current limiters is their near-instantaneous response to overcurrent events, occurring in less than 5 milliseconds, i.e., within a quarter of a voltage cycle. Additionally, these solutions demonstrate environmental friendliness as they operate with cryogenic liquids, primarily nitrogen, an inert gas commonly found in the atmosphere.
Nevertheless, designing and operating network arresters present formidable challenges, as they must function under high transmission line voltages and currents, posing potential risks to sensitive superconducting elements and cryogenic systems. To address this, the distribution of current within the superconducting element over a distance equivalent to the length of thermal diffusion must be homogenous to prevent local thermal power release that could damage the delicate superconducting material.
Encouragingly, progress has been made in achieving this condition with several materials, including bismuth-based solid materials and YBaCuO-type tapes. Research on superconducting current limiters is active in Europe, the United States, and Japan, each focusing on different aspects, from high-power machine interactions in the US to urban energy consumption challenges in Japan.
The growing industrial reliance on computers and specialized equipment necessitates high-quality electricity generation, achievable through concentrated power generation units. These units demand robust protection against grid failures, fueling interest in compact, fast-acting protective devices like superconducting arresters, particularly vital in densely populated urban areas like Tokyo.
Remarkably, China achieved a milestone in December 2005 by deploying a high-temperature superconducting arrester in its power grids. Collaboratively developed by the China Institute of Electrical Engineering, the Technical Institute of Physics and Chemistry, and Yunnan Electric Power Plants, this prototype utilized a “smart” superconductor strip from the American Superconductor Corporation. Since installation, it has effectively suppressed numerous current pulses exceeding rated levels by up to five times, protecting crucial power equipment.
This arrester, operating at 10.5 kV with a rated current of 400 A, was stationed in a power substation near Shanghai, where it successfully mitigated a three-phase grid short-circuit, preserving costly power infrastructure. The plan entails utilizing the arrester for six months, followed by component evaluations to enhance the design before its reintegration into the power grid. The adoption of high-temperature superconductors in power grids, including their application in superconducting arresters, is presently under the scrutiny of the relevant committee within CIGRE, the International Council of Large Electric Systems, headquartered in Paris, dedicated to advancing large electric power systems worldwide.
Superconductivity materials future development
Recently, a breakthrough in the realm of superconductivity has been achieved by Prof. Russell Hemley’s team at George Washington University. They reported a remarkable feat – the attainment of superconductivity at temperatures exceeding zero degrees Celsius. This achievement marks the crossing of a long-standing temperature threshold, bringing us closer to the possibility of harnessing superconductivity in everyday conditions on Earth. The significance of this development cannot be overstated, as it holds the potential to trigger transformative changes in both technology and our daily lives.
Consider, for instance, the ubiquitous issue of electronic devices, including transistors and computers, heating up during operation, resulting in substantial energy losses. If superconductivity were to occur at room temperature, without the need for elaborate cooling systems, we could recover a significant portion of the electricity currently lost. This could revolutionize our energy landscape, with the potential to transmit electricity over long distances with minimal losses. Imagine the environmental benefits of efficient energy transmission and reduced electricity prices, directly impacting consumers.
Notably, there have been reports of Korean scientists exploring superconductors that function even at temperatures exceeding 100 degrees Celsius. Such a development could usher in a revolution, particularly considering that existing superconductors operate at temperatures approaching absolute zero.
However, as Prof. Martinek points out, the excitement surrounding these findings should be approached with caution. While temperature plays a vital role, it’s equally crucial for a superconductor to transmit high-intensity currents and exhibit properties conducive to practical applications, such as wire manufacturing. Many known superconductors demand expensive liquid helium cooling to near absolute zero temperatures, limiting their widespread utilization.
The recent Korean discovery introduces a new family of superconductors, but it’s vital to remember that success in this field typically involves the incremental discovery of better-performing materials within a family. Immediate breakthroughs like this are rare, and competition is fierce, making preemptive announcements the norm.
In the quest for superconductors that function at room temperature, many questions remain unanswered. The challenges in finding such materials are significant, involving computational methods and experimentation. Despite a century of research, the intricacies of superconductivity, especially in newer discoveries, remain a mystery.
Prof. Martinek emphasizes the complexity of the issue, highlighting that nature doesn’t inherently impose temperature barriers on superconductivity. The key lies in maintaining electron pairs, the foundation of superconductivity, at higher temperatures. Additionally, current intensity diminishes with increasing temperature, posing another obstacle in the search for room-temperature superconductors capable of carrying robust currents.
In conclusion, the journey toward revolutionary superconductors operating at room temperature is laden with uncertainty. While the possibility remains tantalizing, the timeline for its realization is uncertain – it could be a decade, half a century, a century, or it may prove elusive. Nonetheless, scientific exploration in this domain persists, driven by the pursuit of groundbreaking discoveries that could reshape our world.
Theory of superconductivity
The groundbreaking theory of superconductivity, known as the BCS theory (named after its creators John Bardeen, Leon Cooper, and J. Robert Schrieffer), emerged in 1950 and earned them the Nobel Prize in 1972. Although it’s a complex theory, we’ll provide a concise overview here.
In typical conductors, the electrical behavior hinges on the most energetic electrons, those near the Fermi energy level. In 1956, Cooper demonstrated that if there’s any attractive interaction between two electrons at this Fermi level, they can form a bound state with a total energy lower than twice the Fermi energy, and these paired electrons are referred to as a Cooper pair.
Now, it might seem counterintuitive for electrons to attract each other, given their identical charges, but this attraction becomes conceivable when we consider the influence of the lattice of surrounding atoms. The mechanism underlying this attraction is depicted in Figure 1: As electron 1 moves through the lattice, it causes the nearby atoms to undergo slight shifts, drawing them closer together due to electrostatic forces. This localized increase in positive charge density catches the attention of electron 2, which is then indirectly attracted towards the region where electron 1 is located. Importantly, the Pauli exclusion principle dictates that these two electrons within a Cooper pair must possess opposite spins.
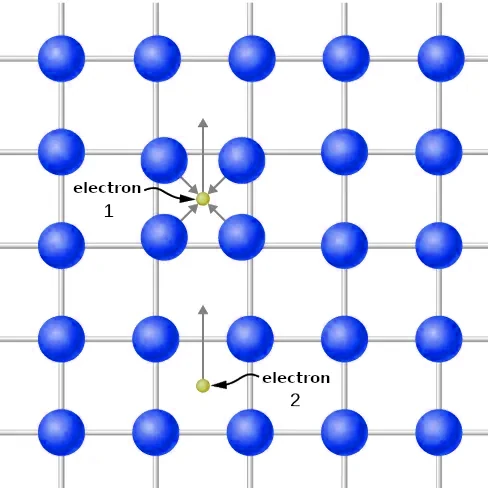
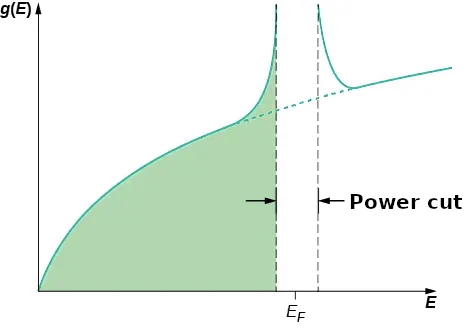
The BCS theory extends Cooper’s idea (which concerns a single pair of electrons) to the entire electron gas. When the transition to the superconductive state occurs, all the electrons begin to form Cooper pairs. On an atomic scale, the distance between the two electrons forming the Cooper pair is quite large. There are usually about 106 other electrons between these electrons, each of which is coupled with some distant electron. Hence we have a strong overlap of Cooper’s wave pairs, which in turn results in a strong correlation of the movement of pairs. All of them move in “equal step” like the members of a marching orchestra. With the transition to superconductivity, the density of states around the Fermi level changes drastically. As shown in Figure 2, an energy break occurs around the EF, because Cooper’s pairs have lower energy than Fermi’s gas of non-interacting electrons. The appearance of this break is characteristic of the superconductive state. If this state is destroyed, then the break disappears and the density of the states becomes the same as for the gas of free electrons.
The BCS theory offers profound insights into the properties observed in superconductors, providing explanations for various phenomena like the Meissner effect, the critical temperature, the critical magnetic field, and, perhaps most remarkably, the complete absence of resistance at critical temperatures. To grasp the latter phenomenon in a simplified manner, we can contrast it with the behavior of normal conductors. In conventional conductors, resistance arises partly from the interactions between conduction electrons and the atomic lattice, with exchanged energies on the order of thermal energy, kBT.
However, in a superconductor, the flow of current is facilitated by Cooper pairs, and the only way for this paired electron vapor to dissipate energy into the lattice is by disrupting it. The separation of just one Cooper pair can halt the collective motion of all pairs, necessitating an energy expenditure of around 10–3 eV, roughly matching the energy barrier. Below the critical temperature, thermal energy is insufficient to initiate such a process, allowing Cooper pairs to traverse the lattice unhindered.
Interestingly, it’s worth noting that superconductivity remains elusive in the most efficient normal conductors, such as copper or silver. The BCS theory helps rationalize this observation. The foundation of the superconducting state lies in the interaction between electrons and the lattice. In these exceptional conductors, this interaction is notably weak, resulting in a sizable Fermi energy. Consequently, it’s reasonable to assume that the electron-lattice interaction in these materials is too feeble to foster the formation of Cooper pairs, rendering the prospect of a superconducting state highly improbable.
How superconductivity works
The superconducting state can be defined by two distinctive properties. Firstly, it exhibits an absolute absence of electrical resistance, denoted as R = 0, implying infinite conductivity. This remarkable characteristic persists at temperatures below the critical temperature (Tc) associated with the superconducting transition. Secondly, it displays ideal diamagnetism, a phenomenon where the magnetic field is expelled from the interior of the superconductor, resulting in a complete absence of magnetic induction within (Bw = 0). These two defining attributes collectively constitute the essence of what we identify as the superconducting state.
Zero resistance
In investigations involving the induction of a current within a sealed superconducting ring, fascinating outcomes emerged. These experiments demonstrated the extraordinary persistence of the current flow, enduring for many years without any measurable decay. This astounding longevity provided an estimate of the electrical resistance, reaching an astonishingly minuscule value of 10–23 Ω*cm. To put this in perspective, it’s a staggering 18 orders of magnitude below the resistance exhibited by copper at room temperature.
To gain further insight, consider Figure 3, which not only illustrates the course of electrical resistance in the superconductor concerning temperature but also outlines the methodology employed to pinpoint the critical temperature, denoted as Tc. These experimental findings underscore the remarkable and transformative nature of superconductivity.
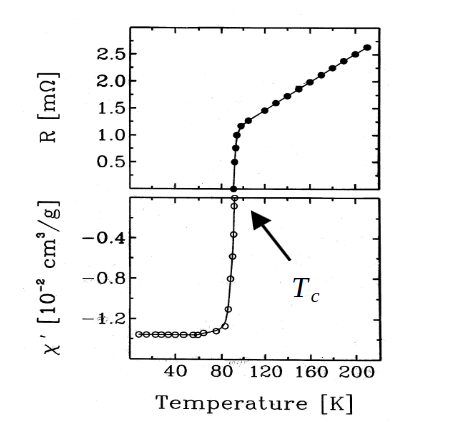
The resistance of the sample decreases to zero, and the susceptibility is negative (diamagnetic) and constant to temperatures below the critical temperature T< Tc.
Perfect diamagnetism
The phenomenon of pushing the magnetic field from within the superconductor is called the Meissner-Ochsenfeld effect. They are presented schematically in Figure 4.
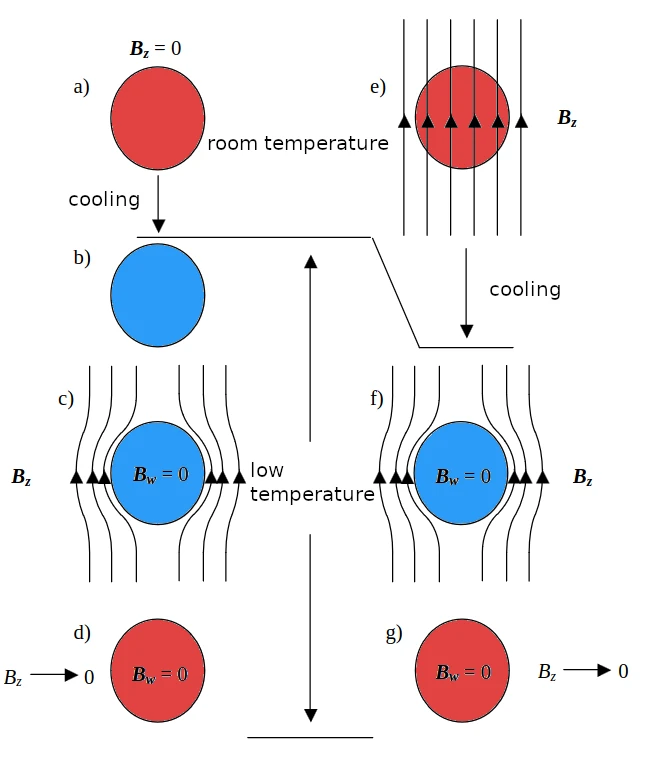
The intriguing phenomenon of negative vulnerability observed in diamagnetism owes its existence to the Meissner-Ochsenfeld effect, a fundamental principle in the world of superconductors. This relationship can be expressed through the equation Bw = Bz + M, where χ, representing vulnerability, equals M divided by Bz, resulting in a value of -1 when Bw reaches zero.
In the timeline spanning from the initial discovery of superconductivity by Kamerlingh Onnes in 1911 up to 1986, the highest recorded transition temperature to a superconducting state stood at approximately Tc ≈ 23K, exemplified by the Nb3Ge compound. However, it wasn’t until 1986 that a significant breakthrough occurred, thanks to the pioneering work of G. Bednorz and K. Müller. They unearthed the phenomenon of superconductivity in materials boasting a perovskite structure, notably in ceramic samples of La2-xBaxCuO, at a temperature of approximately 30 K. Subsequent years witnessed remarkable progress in the realm of novel superconductors, marked by the attainment of increasingly elevated critical temperatures.
As depicted in Figure 3, this progression becomes evident. In 1987, the superconductor YBa2Cu3O7 was synthesized, featuring a transition temperature Tc of 92 K, surpassing the boiling point of liquid nitrogen. In the following years, additional high-temperature superconductors, known as HTS materials, emerged. These materials incorporated copper-oxygen bonds and included bismuth, tantalum, and mercury-based superconductors, marking a transformative phase in the exploration of superconductivity.
Superconductor in magnetic field
In the realm of superconductors and their behavior in the presence of an external magnetic field, the pioneering work of A. Abrikosov unveiled a crucial distinction between two fundamental types: Type I and Type II superconductors. Type I superconductors exhibit the remarkable ability to expel the entire magnetic flux from their interior. Conversely, Type II superconductors, characterized by their unique properties, are capable of pushing the magnetic flux aside in fields smaller than a critical threshold known as the first critical field (Hc1). Beyond this critical field, an intriguing phenomenon occurs – the magnetic flux partially infiltrates the material in the form of vortices, while the region outside the wire maintains its superconducting state intact. This distinctive characteristic of Type II superconductors allows them to play a pivotal role in the lossless transmission of electric current, marking a significant advancement in the practical applications of superconductivity.
Superconductors I type
Superconductors of type I, below Tc, push the magnetic stream completely out of their interior until they return to normal. This transition is a phase transition of the first type. Below the critical field Hc inside the sample magnetic induction B = 0, and thus from the dependency:
we get the magnetization of the superconductor in a stack of perfect diamagnetism:
whereas the magnetic vulnerability of the superconductor, i.e. the ratio of magnetization to the intensity of the field is
Figure 5 below shows the change in M magnetization in the function of the external magnetic field Hz for this type of superconductors.
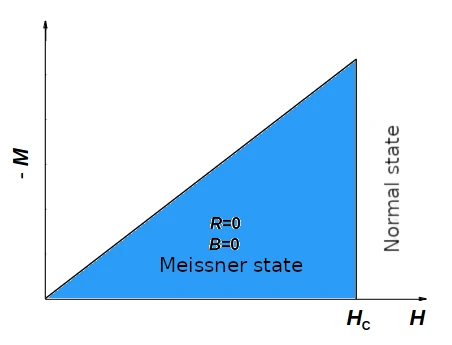
Within the realm of superconductivity, there exists a fascinating phenomenon where the magnetic field can be actively expelled from the interior of the superconductor, provided it does not surpass a specific threshold referred to as the superconductor critical field, denoted as Hc. This critical field value is contingent upon various factors, including temperature and the specific type of superconductor under consideration. When examining the relationship between the critical field Hc and temperature, we find that, for type I superconductors, experimental observations reveal a reasonably accurate description of this dependence, offering valuable insights into the intricate behavior of these remarkable materials.
where H0 is the extrapolated value of Hc for T → 0. Below is a phase chart for type I superconductors.

Effect of the de-magnetization factor and intermediate state
The superconducting transition to the normal state abruptly occurs when the applied magnetic field reaches a critical value, and this phenomenon is particularly prominent in thin samples, such as elongated rod-shaped specimens oriented parallel to the applied magnetic field. However, when dealing with samples of different shapes, an additional factor comes into play – the demagnetization factor of the sample. In magnetic fields smaller than the critical field, the interior of the superconductor undergoes a fascinating transformation, partitioning into regions characterized by both superconducting and normal-state behavior. This intriguing coexistence of states in type I superconductors is referred to as the intermediate state.
For rotary ellipsoid-shaped samples, the internal field within the sample, denoted as Hw, takes on a specific value, which can be determined as follows:
where Hz is the external field applied, M is magnetization and n is the de-magnetization factor. For the superconductor in the Meissner state we have : M = – Hw, i.e.
This means that in some parts of the sample the intensity of the internal field exceeds the value of the external field and therefore this part of the specimen returns to the normal state in fields smaller than Hc. The diagram of magnetization of a superconductor with a non-zero de-magnetization coefficient looks schematically.
The intermediate state is achieved in a field Hc’ smaller than the critical field. Using the dependency M = – Hw and inserting the vulnerability value of the ideal diamagnetic given by the formula x = -1 after submitting them to the formula Hw we get:
And finally, when we base the formula on the relationship M = χ. H and simplify the formula, we get an expression on the dependency of the sensitivity to the demagnetization coefficient:
In this formula, the symbols χ and χ0 hold significance, representing the magnetic susceptibilities of a sample with distinct demagnetization coefficients—one indicating a non-zero value and the other denoting a value of zero. As we delve into the implications of this equation, it becomes evident that the susceptibility in the Meissner state experiences an augmentation for samples characterized by a non-zero demagnetization factor. Consequently, this augmentation in susceptibility leads to a broader range of magnetic transitions that can be observed in such samples.
Type II superconductors
Superconductors of Type I primarily manifest as pure metals, while their Type II counterparts are frequently composed of alloys comprising various metals or exhibit characteristics associated with “multi-element” superconductors. Type II superconductors introduce a nuanced complexity by showcasing two distinct critical fields at a given temperature, known as Hc1 and Hc2. Within the range demarcated by these critical fields lies what’s referred to as the “mixed state.”
The lower critical field, Hc1, denotes the threshold below which Type II superconductors, akin to their Type I counterparts, maintain the Meissner state. However, as the applied magnetic field surpasses this point, a phenomenon known as the mixed state emerges. In Type II superconductors, this entails the coexistence of superconducting regions intermingled with normal areas, forming slender filaments of the normal state aptly termed vortexes, spirals, spiral threads, or fluxoids.
Remarkably, the density of these vortices escalates with the increasing external magnetic field. Upon reaching the second (upper) critical field, Hc2, the entire superconducting material transitions back to the normal state. As a result, the M(H) chart, which characterizes the magnetic response, exhibits a distinct pattern compared to its Type I superconductor counterpart. (Refer to Figure 5 for Type I superconductors in comparison to Figure 7). This intricate interplay between critical fields and the mixed state underscores the intricate nature of Type II superconductors.
References:
https://openstax.org/books/fizyka-dla-szk%C3%B3%C5%82-wy%C5%BCszych-tom-3/pages/9-8-nadprzewodnictwo
https://winntbg.bg.agh.edu.pl/rozprawy2/10520/full10520.pdf












