Coil / Inductor – Basics, Definition and Parameters

Coil / Inductor

Inductor (also named coil or reactor) is a passive electronic component, which manufacturing process is based on winding a given number of conductor windings on a particular surface e.g. a ring (which creates a toroidal coils, a roller (solenoids) or a plane (spiral, flat coils). In addition, on the outside/inside of the coils there can be created a core made of a magnetic, diamagnetic or ferromagnetic material. 

In the matter of the fact, that coil is the inertial element, it stores energy in the generated magnetic field. Applying an inductor with the capacitor in one circuit results in the resonant circuit (which is one of elementary electronic circuits). Coil that is powered by direct current is commonly called electromagnet, which is used to generate magnetic field or its compensation (balancing e.g. during demagnetization). In the circuit of alternating current, the coil induces a current, thus it causes a delay of its voltage in relation to the phase voltage and the total resistance increase. Inductor placed in electrical systems has a number of properties, for example except generating a magnetic field, it can induce a current as well as affect on the current and voltage phase. The coil symbol is denoted by the letter L – as its inductance. 

Coil – Technical parameters

Inductor in the direct current circuits plays the role of the resistive component (resistance depends on the material from which it was made). However, when the frequency has a value greater than 0 (ω > 0), the resistance of the coil is called electrical reactance (usually denoted with the letter X).

Reactance of the coil

ω – angular frequency

Impedance of the coil

When we deal with an ideal inductor, the impedance is equal to the product of its reactance and the imaginary unit:

Inductance of the coil

Inductance is a fundamental electrical parameter that describes a coil, marked with the “L” letter. It is defined as the current (magnetic induction vector stream) flowing through the coil. The unit of inductance is Henr [H]. Formula is presented below:

– a magnetic induction flux,

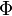
i – the current intensity flowing through the inductor.

The shape of the coil, thickness of the wire used in the component and the number of turns of this wire has direct influence at k factor. The inductance of the coil is also dependent of the magnetic properties of the core. 

Induction flux of the magnetic field flowing through the inductor is described by the formula:

L – inductance of the coil,
i – the current flowing through the coil.

The current flowing through the conductor of a given intensity generates magnetic field at the same time. The energy of this field is numerically equal to the work needed to produce it, which is: 

L – inductance of the coil,
I – the current flowing through the coil,
B – magnetic induction,
V – the volume of the coil (the focus of the B induction).

The electromotive force (EMF) that is inducing in the inductor is described by the formula:

If we assume that the inductance of the coil is constant (as it’s true for most electrical circuits), the above formula can be written as:

 – magnetic induction flux,

i – current intensity flowing through the coil,

L –induction of the coil,

e – electromotive force,

t – time.

Coil constant

Coil constant for the DC current corresponds to the inductance:

H – the intensity of the magnetic field,
I – current intensity.

Coil – Series and parallel connections

Inductors can be combined like resistors and capacitors in series and parallel configurations and used in e.g. input voltage LC filtering systems in digital circuits (“before” microcontrollers).

In the series connection, the same curent value flows through every component. However, it is worth noting that each of them can have different voltage. Total inductance of such system is given by:

Inductors connected by parallel connection can be replaced by one with a total inductance given by formula: 

Properties shown above apply only when the magnetic field of each of the coils does not affect each other.